I found this finance concept when studying for the CFA exams. Looking at both geometric and arithmetic formulas can help you calculate investment returns. And you should know when to use one over the other.
I’ll show you the formulas and an example below. Also, if you’d prefer to see another explanation, here’s a short video…
Geometric vs. Arithmetic Returns
Feel free to check out the comments on my video to learn more. If you have any finance or career questions, post a comment and I’ll respond. I like sharing what I’ve learned 😊
Arithmetic Formula
What is arithmetic mean? Let’s start with this common return formula…
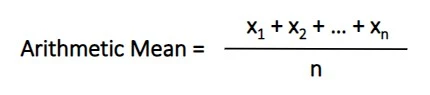
To calculate, sum up all the returns and then divide by the number of returns.
This gives you the arithmetic mean. You might have learned this along with the median and mode of a sequence.
Geometric Formula
What is geometric mean? This formula factors in compounding returns…
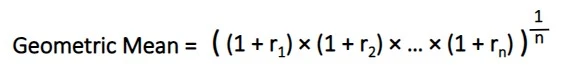
To start, add one to all the returns. For example, -7% would become 0.93 (1 + -0.07) and a positive 9% return is 1.09 (1 + 0.09). This is a step that many people miss and struggle to understand.
For clarity, imagine you start with $100. You’re starting with one (100%) times your investment. If it goes down 7%, you’d have $93 (0.93) of your initial investment.
For the next step, take all those numbers and multiply them together.
Then for the second to last step, take that result and raise it to one over the number of returns. If you’re working with annual returns, this step annualizes the number.
To turn it into a percentage, subtract one and times by 100.
At first, this might seem complex but with an example, it should make more sense. It took me awhile to learn and it was one of hundreds of finance formulas to pass the CFA exams. If you’re considering that route, check out my thoughts on Is the CFA Worth It?
Geometric vs. Arithmetic Return Example
Let’s calculate these averages for an investment portfolio that starts at $100,000. In the first year it jumps 10%. Then in the second year it drops 7%. And in the third year, it climbs by 5%.
To find the arithmetic mean, take 10% + -7% + 5% and you get 8%. Then from there, divide 8% by 3 (the number of returns). This gives us an average annual return of 2.67%.
For geometric mean, start by taking (1 + 0.1) × (1 + -0.07) × (1 + 0.05). Simplified, this becomes 1.1 × 0.93 × 1.05 and results in 1.07415. To get the average annual return, calculate 1.07415 ^ (1/3) and you get 1.0241. To make it a percentage, subtract one and times by 100. This gives us an average annual return of 2.41%.
With this example of arithmetic vs. geometric returns, they’re not the same. And this is usually the case…
Why is Geometric Return Less Than Arithmetic?
If you want to find the average score for a test, arithmetic makes sense.
On the other hand, it’s better to use geometric when dealing with dependent, subsequent events. For example, annual investment returns. Let’s continue with the example from above…
In the first year, the $100,000 portfolio jumped 10% to $110,000. Then starting the second year at this new value, it dropped 7% to $102,300. Then in the third year it climbed by 5% to $107,415.
Let’s compare the real growth to how $100,000 grows at the geometric vs. arithmetic returns that we calculated (in three years)…
| Real | $107,415 |
| Arithmetic | $108,226 |
| Geometric | $107,406 |
As you can see, geometric returns give us an end value that’s closer to the real portfolio. And the only time you’ll see the same number for both geometric and arithmetic is when the returns are the same every year. For example, if the real portfolio grows by 10% every year.
Otherwise, geometric mean will always be lower than arithmetic. Geometric mean factors in compounding growth. And this is a vital concept for finance. Your investment returns are nonlinear going from one year to the next.
For a next step, here’s another short article that covers the Cumulative Annual Growth Rate (CAGR) formula. Are you studying for the CFA exams? How about a finance class? Or are you trying to improve your investment returns? Feel free to comment on any of my videos with questions.