The harmonic mean formula helps you calculate an average. This is one of many finance concepts I learned when studying for the CFA exams. But as an investor, when should you use harmonic mean?
To get a better idea of how harmonic mean works, check out my breakdown of Geometric vs. Arithmetic Formulas. Those are more common formulas that can help you understand harmonic averages…
Harmonic Mean Formula
How do you calculate harmonic mean? Here’s the formula…
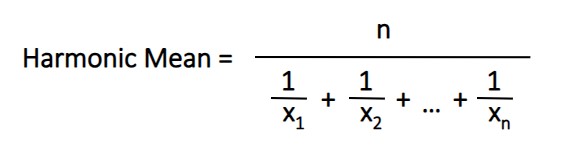
To find the harmonic average, start with the total number n as the numerator. For the bottom of the equation, you sum up the reciprocals of each number. Let’s look at an example…
Harmonic Mean Example
Let’s say you invest $10,000 each year for three years into the same company. There’s a lot that can happen in a year and the share price changes. Here are the prices you lock in each year…
| Year 1 | $15 |
| Year 2 | $30 |
| Year 3 | $25 |
What’s your average cost basis per share?
One approach would be to calculate the arithmetic mean. This would give you (15 + 30 + 25) / 3 = $23.33. However, this doesn’t calculate your true average buying price. For a more accurate cost basis, you can use the harmonic mean…
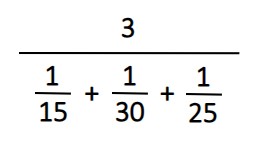
This example gives you an average price of $21.43. To see why this is more accurate, let’s look at the full investing example. The harmonic mean formula gives you an easier way to calculate this…
Over the three years, you invest a total of $30,000. In the first year, you buy 667 shares. That’s the first $10,000 divided by $15 per share. In the second year, you buy fewer shares because the cost is higher at $30. You can buy half as many shares…
| Year 1 | 667 shares |
| Year 2 | 333 shares |
| Year 3 | 400 shares |
In total, you’ve bought 1,400 shares. Then to find the real average cost basis per share, take the total investment of $30,000 divided by 1,400. This gives you $21.43 and matches the harmonic mean.
When to Use Harmonic Mean
The example above shows a good use case. When dealing with recurring investments, harmonic average is often the better way to go. Said another way, it’s useful when you’re dollar cost averaging.
For a non-investing example, harmonic mean is good to find the average speed when traveling. For example, if you drive one way at 60 MPH and return at 80 MPH, your average speed is not the arithmetic mean of 70 MPH. Instead, the harmonic mean gives you an average speed of 68.6 MPH.
It’s also good to keep in mind that you can’t calculate harmonic mean if one of the values is zero. Let’s now look at a slightly different version of this formula…
Weighted Harmonic Mean Formula
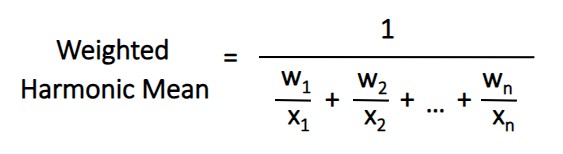
The weighted harmonic mean formula is similar to the one above. Let’s dive into an example to see the difference…
Weighted Harmonic Example
Similar to the example above, let’s say you invest each year for three years. However, this time it’s not the same amount each year. You invest $10,000 in year one, $20,000 in year two and $50,000 in year three.
Using the average share prices from the example above, here’s the weighted harmonic formula…
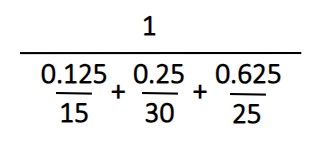
This gives you an average share price of $24. Also, a friendly reminder, if you’re testing this calculation, don’t forget parentheses for order of operations.
The main changes are swapping out the ones for the investment weights. To find the weights, divide each investment by the total of $80,000 over the three years. As a result, the first $10,000 divided by $80,000 gives us a weight of 0.125. That’s followed by 0.25 and 0.625 for $20,000 and $50,000, respectively.
You also swap out n on top for one. That’s because you’ve weighted each investment below and those add up to one.
When it comes to investing, there are many moving pieces. This weighted harmonic mean example is more realistic to what you’ll see when investing.
CFA Formulas for Investors
Are you learning these formulas for the CFA exams? I’ve passed the three exams and shared an article: Is the CFA worth it? It’s a quick read and you’ll also find some useful study tips.
The harmonic mean formula is good to know. And now that you know when to use it, it’s good to add more tools to your tool belt…
I’ve learned many hundreds of finance formulas and have put together complex DCF models. However, I’ve moved towards simpler valuation techniques. Here’s one of my favorites: GGM Calculator. If you have any questions, feel free to comment on any of my videos.