What’s the average? There are many ways to calculate an average. You’ll likely recall mean, median and mode. And the most common is mean. However, that breaks down further into the three Pythagorean means.
Each of these means is useful in different situations…
Three Pythagorean Means
- Arithmetic Mean
- Geometric Mean
- Harmonic Mean
A good rule of thumb is that arithmetic mean will always give you the largest average. That’s followed by geometric and harmonic means. This can be true for negative numbers as well…
Harmonic Mean ≤ Geometric Mean ≤ Arithmetic Mean
The only time you’ll see these means equal to each other is when all the numbers in the sequence are the same. In these unique cases, each of the three Pythagorean means gives you the same answer.
Let’s dive deeper into each mean and when to use them. To start, let’s review the most common average. When most people calculate an average, they use the arithmetic mean without knowing its full name…
Arithmetic Mean
For this example and the ones below, let’s find the three Pythagorean means for this set of numbers…
Numbers for Examples Below = ( 2, 8, 6 )
To calculate the arithmetic mean, simply sum up the numbers and divide by the total count of numbers. Here’s the arithmetic mean formula…
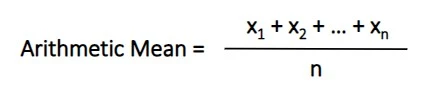
Plugging the numbers into this equation gives us…
( 2 + 8 + 6 ) / 3 = 5.3
This is the largest result you’ll see when calculating the three Pythagorean means. You’ll see this as we use the same numbers with the other formulas.
When do you use arithmetic mean? It’s best when finding an average for independent events. For example, finding the average score for an exam. The first student’s exam score is not dependent on the last student’s score.
This type of average is useful in many cases and is followed by the geometric mean…
Geometric Mean
To calculate the geometric mean, multiply all the numbers together. Then take that result to the nth root. Here’s one way to show the geo mean formula…
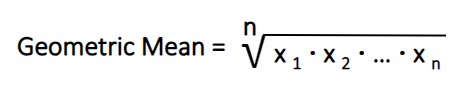
Depending on how you calculate these formulas, don’t forget parentheses to control the order of operations. Excel and other spreadsheets have these formulas built in as well. Here’s using the same example numbers from above…
( 2 × 8 × 6 ) ** ( 1 / 3 ) = 4.6
This geo mean gives us 4.6 and it comes in well below the arithmetic mean of 5.3. But why is this the case?
When do you use geometric mean? It’s best when finding an average for most subsequent dependent events. For example, this could be how your investment portfolio grows over many years…
If you invest $10,000 at the start and it grows 10% in year one, you’d be up $1,000. You’d then start year two with $11,000. If you saw another 10% increase in year two, you’d be up $1,100. That brings your portfolio up to $12,100 to start year three.
The total nominal returns each year are dependent on the previous year’s change. Your results compound and the geometric mean takes this into account. That’s why it calculates a smaller number than the arithmetic formula.
Investments and many other areas of the natural world grow in a non-linear way. And said another way, it’s exponential growth. The changes in human and animal populations follow a similar pattern.
Now you know two of the most common Pythagorean means. But to gain an even better understanding, check out this deep dive into Geometric vs. Arithmetic Formulas. There’s another step to the geometric formula for investment returns.
Harmonic Mean
This is the least common of the three Pythagorean means. Still, it’s good to know when to use it. Here’s the formula…
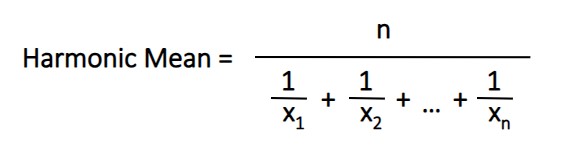
To find the harmonic mean, count the total of numbers n and use that as the numerator. For the bottom of the equation, sum up the reciprocals of each number. Here’s how this works with the example numbers from above…
3 / ( 1 / 2 + 1 / 8 + 1 / 6 ) = 3.8
The harmonic mean gives us the smallest average. That’s because the formula reduces the impact of large outliers and can give more weight to smaller ones.
When do you use harmonic mean? It’s best when finding an average for certain subsequent dependent events. For example, finding the average speed when traveling…
If you drive half a distance at 60 MPH and the second half at 80 MPH, your average speed is not the arithmetic mean of 70 MPH. Instead, the harmonic mean gives you an average speed of 68.6 MPH.
There’s more to this equation as well. For example, check out this deep dive that also shows the Weighted Harmonic Mean Formula. I’ve highlighted when to use this formula for investors.
If you have any questions about the three Pythagorean means, feel free to reach out. You can comment on any of my YouTube videos. And if you found this useful, I’d really appreciate it if you’d share it with others. Because that helps me as a small content creator.